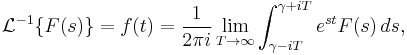Inverse Laplace transform
Contents |
Mellin's inverse formula
An integral formula for the inverse Laplace transform, called the Bromwich integral, the Fourier–Mellin integral, and Mellin's inverse formula, is given by the line integral:
where the integration is done along the vertical line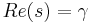 
in the complex plane such that 
is greater than the real part of all singularities of F(s). This ensures that the contour path is in the region of convergence. If all singularities are in the left half-plane, or F(s) is a smooth function on - ∞ < Re(s) < ∞ (i.e. no singularities), then can be set to zero and the above inverse integral formula above becomes identical to the inverse Fourier transform.
In practice, computing the complex integral can be done by using the Cauchy residue theorem.
It is named after Hjalmar Mellin, Joseph Fourier and Thomas John I'Anson Bromwich.
Post's inversion formula
An alternative formula for the inverse Laplace transform is given by Post's inversion formula.
See also
References
- Davies, B. J. (2002), Integral transforms and their applications (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-95314-4
- Manzhirov, A. V.; Polyanin, Andrei D. (1998), Handbook of integral equations, London: CRC Press, ISBN 978-0-8493-2876-3
- Boas, Mary (1983), Mathematical Methods in the physical sciences, John Wiley & Sons, p. 662, ISBN 0-471-04409-1 (p. 662 or search Index for "Bromwich Integral", a nice explanation showing the connection to the fourier transform)
External links
- Tables of Integral Transforms at EqWorld: The World of Mathematical Equations.
- Rational inversion of the Laplace Transform
This article incorporates material from Mellin's inverse formula on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.